トーナメントの組合せ
スポーツの大会でよく行われるトーナメントですが、その組合せは一体何通りあるのでしょう?
ここでは、A〜Hの8チームが参加をするとします。
トーナメントの表も,次の図の通りであるとします。
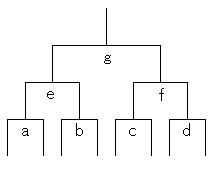
| 例題1 | 1回戦から決勝の全ての試合において,右が一塁側、左が三塁側と区別をつけるときの組み分けの方法は何通りか。
8チームの野球のトーナメントの、フリー抽選の状態を想定しています。
| ||||
| 例題2 | 8チームが対等で、abcdそれぞれの左右に区別はつけないが、abcdには区別があるときの組み分けの方法は何通りか。
サッカーのトーナメント(ホームでもアウェイでもない会場での開催)がこのような感じでしょうか。
| ||||
| 例題3 | 8チームが対等で、aとb,cとd,eとfには区別をつけないときの組み分けの方法は何通りか
剣道や卓球などのように、1会場での同時開催が可能な場合はこれになります。 それでは、さらに条件を付け加えてみましょう。
| ||||
| 例題4 | AとBが決勝まで当たらないような組合せは何通りか。
シード制などでは、このような条件がつくと思います。 abcdそれぞれの左右に区別はつけないが、abcdには区別があるとき aとb,cとd,eとfには区別をつけないとき
例題5 | AとBがP県、CとDがQ県、EとFがR県、GとHがS県の代表で、 | 同じ県代表ののチーム同士が決勝まで当たらないようにする組合せは何通りか。
どの設定においても,PQRSを2つずつ用意し、aとbで1個ずつ、cとdで1個ずつ振り分けます。 abcdそれぞれの左右に区別はつけないが、abcdには区別があるとき aとb,cとd,eとfには区別をつけないとき 32×23=72通りとなります。 関連項目;トーナメントの優勝確率について
ちなみに、夏の高校野球の組合せですが、 | 東ブロックの24校と、西ブロックの25校に別れ、 同地区が1回戦で当たらないように抽選します。 この場合の抽選結果の場合の数は25!×24!ですから、実に9.62×1048通りあります。 1塁側と3塁側に区別をつけてしまうと、さらに224倍ですから、1.61×1056通りに跳ね上がります。 9.62×1048通りの全てを、厚さ0.1ミリの薄い紙に1枚ずつ書いて重ねると、 1光年を9.46×1015メートルとしても、1.01×1029光年に達します。 宇宙の大きさは150億光年と推定されていますが、 それでも3.30×1018個分になります。膨大すぎる・・・ 1枚10秒の速さで書けたとしても、1.82×1044年、 宇宙の歴史が130億年だとすると8.80×1034回繰り返さなくてはいけないそうです。 単純に同じ県の組合せ、と考えた場合は西ブロックを固定します。 それでも25!=1.55×1025通りの組合せがありますから、 同じ要領で厚さ1ミリの紙に書いていくと、79,708光年になります。 銀河系の直径がおよそ10万光年ですから、まあ、そのような感じです(意味不明) 例えば大阪代表と神奈川代表が初戦でぶつかる確率だけだったら、1/25となりますから、 普通は25年周期で考えるのでしょうけど・・・ | |