トーナメントに関する確率

トーナメントの表は，次の図の通りであるとします。

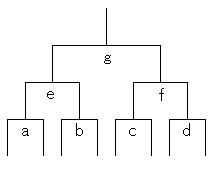
全ての対戦結果の確率が１／２だとつまらない（？）ので、
各チームの勝率を次の表のようにまとめておきます。

○　ＡとＨが直接対戦するときは、どちらが勝つのも１／２ ○　ＡとＨの両チームの、その他の試合で勝つ確率は２／３ ○　Ｂ〜Ｇチーム内では、どの組合せでも１／２

この条件下で、Ａチームの優勝する確率と、Ｂチームの優勝する確率を、
それぞれ求めてみたいと思います。

例題１

Ａがaの左、Ｈがdの右と、シード扱いで固定され、 他がフリーの抽選であるとき ＡとＨが決勝まで当たらない場合を考えてみましょう。 まず、Ａが決勝まで進む確率は(2/3)2＝４／９となります。 Ｈが決勝まで進む確率も４／９ですから、 Ｈと決勝で対戦して優勝する確率は、(4/9)×(1/2)＝2/9となります。 一方、決勝戦がＨでない確率は残った５／９だけあるはずです。 決勝戦がＨでなく、Ａが優勝する確率は(5/9)×(2/3)＝10/27となります。 よって、Ａが優勝する確率は(4/9)×{(2/9)+(10/27)}＝64/243となります。 トンチが効けば、Ｈの優勝する確率も64/273であり、その他のチームが勝つ確率は、 (243-128)/243＝115/243ですから、Ｃの優勝確率はこれを等しく６で割り、115/1458となるはずです。 本当にそうなのか、実際に検証して見ましょう。 初戦でＡまたはＨと対戦するとき 抽選の結果でこのようになる確率は２／６＝１／３です。 初戦がＡだとすると、これに勝つ確率は１／３、２回戦で勝つ確率は１／２なので、 初戦がＡ（Ｈ）で決勝に進む確率は１／１８となります。 初戦がｂまたはｃのブロックのとき 抽選でこのようになる確率は２／３です。 以下、bのブロックに入ったとして話をすすめます。 １回戦に勝つ確率は１／２です。 ２回戦でＡと当たる確率は２／３なので、 ２回戦でＡと当たって決勝に進む確率は２／３×１／３ ２回戦でＡと当たらずに決勝に進む確率は１／３×１／２ 以上より、初戦でｂまたはｃのブロックから決勝に進む確率は、 (2/3)×(1/2)×{(2/9)＋(1/6)}＝7/54となります． 以上のことから、Ｃチームが決勝に進む確率は、 (1/18)+(7/54)＝10/54＝5/27となります。 決勝でＨと対戦して勝つ確率は(4/9)×(1/3)＝4/27， その他のチームと対戦して勝つ確率は、(5/9)×(1/2)＝5/18なので、 Ｃチームの優勝する確率は，(5/27)×{(4/27)＋(5/18)}＝115/1458となり、 予測が正しいことが示せました。 「強豪校」が優勝する確率は128/243で、その他の学校が優勝する確率も115/243ありますから、 （後者は６校がかりですが、）確率はだいたい半々とみられるようです。

例題２

完全なフリー抽選のとき Ａはどこでも良いので、aの左として構いません。 １．初戦でＨと対戦するとき 抽選でこうなる確率は１／７なので、(1/7)×(1/2)×(2/3)×(2/3)＝2/63となります。 ２．Ｈがｂに入ったとき 抽選でＨがｂに入る確率は２／７です。 Ａが１回戦と決勝で勝つ確率は共に２／３となります。 ２回戦でＨと当たって決勝に進む確率は２／３×１／２ ２回戦でＨと当たらずに決勝に進む確率は１／３×２／３ですから， (2/7)×(2/3)×(2/3)×{(1/3)＋(2/9)}＝40/567となります。 ３．Ｈがｃまたはｄに入ったとき 抽選の結果このようになる確率は4/7で、例題１の結果より， (64/243)×(4/7)＝256/1701となります。 以上より、(2/63)＋(40/567)＋(256/1701)＝(54＋120＋256)/1701＝430/1701 となります。 他チームの優勝確率の合計は、(1701−860)/1701＝841/10206ですから、 Ｃチームの優勝する確率はこれを６で割った841/10206となります。（検証略） 64/243=448/1701なので、Ａにとってはシード制のほうがちょっと有利となります。

目次へ