お菓子のおまけが全て揃う確率は?
問題:
今、あるお菓子のおまけを全種類揃えたい。
ところがこのおまけ、商品に附属していてどの種類のおまけが出るか買うまで分からない。
どの種類のおまけも等確率で出て、ハズレはないものとする。
1回につき1個ずつ買い続けるとき、
n回目に初めて全種類が揃う確率を求めよ。
なお、おまけの種類数は解答者に任せる。
この問題は東工大2年、川喜田さんが投稿してくださった問題です。
本当は全て揃うまでの個数の期待値の問題なのですが、
難問なのでここでは確率のみにしぼって扱います。
最後の「種類数が未定である」のが曲者ですね(笑)
これは部屋分け問題で行った、
「9人を2つ(3つ)のグループに分ける方法」と同じ考え方がベストだと思いました。
まず、2種類だとどうなるでしょうか。
おまけがA、Bだとします。
最後にBが出るとして、最後に2倍しても矛盾は生じません。
n−1回Aが出つづけ、最後にBが出る確率は、
(1/2)n-1×1/2
よって、最後に当たるのがAである場合も同様に確からしいので、
(1/2)n-1×(1/2)×2
=(1/2)n-1となります。
次に、3種類の場合はどうなるでしょうか?
おまけがABCであるとします。
これも最後に当たるのがCであるとします。
直前のn−1回まではABのみが出つづける場合の数は、
1回1回について2通りずつ有り得るので2n-1とおりですが、
A(またはB)のみが出つづける場合も含んでいるので、(これではn回目でそろえることが不可能ですから)
2n-1−2通りとなり、その確率は、
(2n-1−2)/3n-1
最後にCが当たる確率1/3をかければ良いのですが、2種類のときと同様、この後3をかけるので、
相殺されて上の確率がそのまま答となります。
4種類にも挑戦してみましょう。
おまけがABCDであるとし、最後にDが出るとして後に4倍して構いません。
n−1回目(n≧4)までに、ABCの全種類が揃う確率を考えます。
3種類を無作為に取った場合の数は3n-1通りあり、
部屋分け問題の時のように、引いていきます。すると、
3n-1−3C2(2n-1−2)−3C1
=3n-1−3×2n-1+3通りですね。
5種類とした場合
同様に考え、さらに一般性も意識します。部屋は「空き部屋の選び方」に直しておきます。
4C04n-1−4C1(3n-1−3×2n-1+3)−4C2(2n-1−2)−4C3
=1×4n-1−4×3n-1+6×2n-1−4
一般に,m+1種類のおまけがn回目で揃う確率は,
最後に0×m-1Cm-1が隠れていると考えれば、
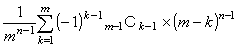 となるようではありませんか?
となるようではありませんか?
それではこれを数学的帰納法で証明してみます。
m=2のときは、1/2n-1となり、正しいですね。
mのときまで正しいとして、m+1のときが正しいことを証明します。

全て揃うまでの個数の期待値の問題へ
目次へ
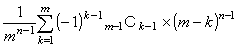 となるようではありませんか?
となるようではありませんか?