さて、n回目で揃う確率は、
よって、求める期待値は、
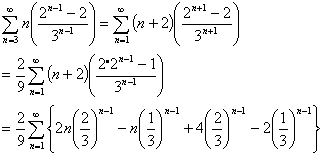
ここで、無限級数の公式を用いると、
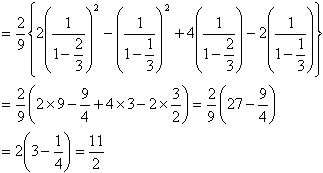
(おわり)
この問題は東工大2年、川喜田さんが投稿してくださった問題です。
これが原文で、期待値でなく、「n回目で揃う確率」とした問題はこちらで扱いました。
さて、期待値となると何が難しいかというと、
いくら2種類でも運が悪ければ100個、200個と買いつづけなければならない可能性もあるからです。
早い話が、無限級数の問題になってしまうわけです。
無限級数に関してこちらに収めておきました。
特に後者の(等差数列)×(等比数列)型の無限級数の知識が必要となりますから、
事前に必ず読んでおくことをお勧めします。
まずは3種類に挑戦したいと思います。
さて、n回目で揃う確率は、![]() でした。
でした。
よって、求める期待値は、
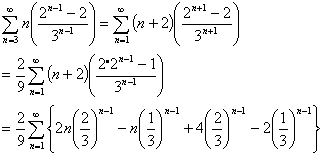
ここで、無限級数の公式を用いると、
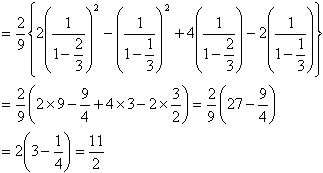
(おわり)
それでは、今度は4種類の場合を考えてみましょう。

この予想が正しいかは疑問が残りますが、正しいとして続けます(笑)
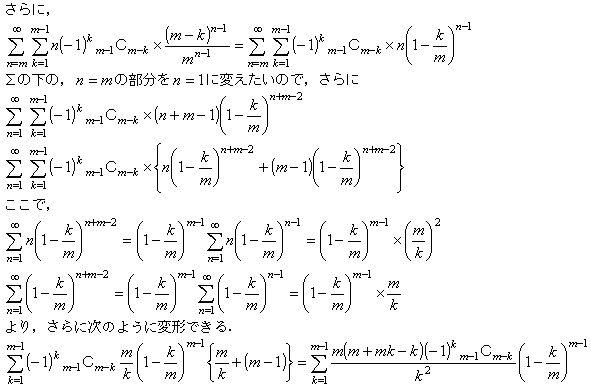
これを更に簡単にできるのかどうかが分からず止まってしまいした。
あとはコンピュータにお任せすれば(For Loopを作ることで)計算できます。
なお、1−2−3マクロによれば、次のようになるようです。
| 種類 | 個数の期待値 |
|---|---|
| 3 | 5.5 |
| 4 | 8.333 |
| 5 | 11.42 |
| 10 | 29.29 |
| 50 | 224.96 |
| 100 | 508.60 |
| 1000 | 2.82*10110 |
悩んでいたところに救世主、pekarinさんが登場!!
発想の転換…あるおまけが当たるまでの期待値を考える。

この式はこれ以上は簡単にできないのですが、先ほどの計算結果と比べるとどうなるでしょうか?
| 種類 | 個数の期待値 | |
|---|---|---|
| 私の式 | pekarinさんの式 | |
| 3 | 5.5 | 5.5 |
| 4 | 8.333 | 8.333 |
| 5 | 11.42 | 11.42 |
| 10 | 29.29 | 29.29 |
| 50 | 224.96 | 224.96 |
| 100 | 508.60 | 518.73 |
| 1000 | 2.82*10110 | 7485.5 |