樹形図について

数えなければならないものと計算で済むものの違い
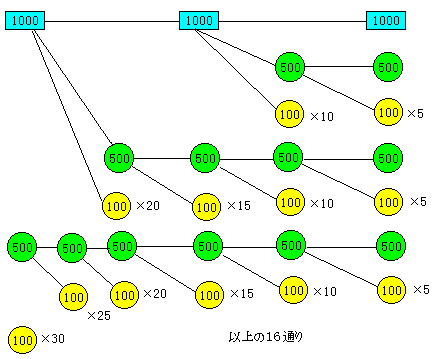
世間には、いろいろな「場合の数」が存在します。
「○○を△△したいけど、何通りか方法がある。」というのが、そのようなものです。
大きく分けると、「数えるしかないもの」と「計算できる」ものがあります。
計算、予測が困難なものの例
例１；３０００円を千円札、５００円玉、１００円玉を使って支払う方法

簡単な計算（１つの公式）で済むものの例
例２；４個の異なる球を１列に並べるときのならべかた

では、どういう時に計算できて、どういう時に数えるしかないのでしょうか。
これは、樹形図「枝別れの仕方」が、規則的であるかどうかで決まります。
もちろん、ベンゼン環の異性体など、列挙してしまったほうが早いものもあります。

例１の樹形図

樹形図を作る上で大切なことは、「漏らさず・ダブらず」です。
ある程度、結果を予測しないと、普通に計算するよりも大変です。

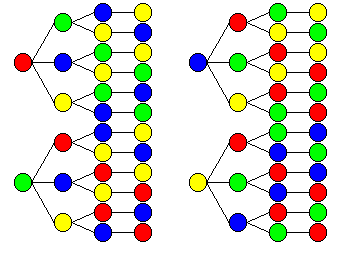
例２の樹形図

例２のように、樹形図の枝別れの仕方が、必ず同じものは原則１つの公式で計算できます。
例２の状態を「ｎ個の異なるものからｒ個とって並べた順列」といい、
nPrと書きます。（詳しくはこちら） ちなみに、例１が「計算できない」のではありません。
ただし，その方法はとんでもなく難しいですが・・・（気になる人はこちら）

Back