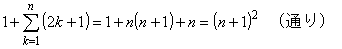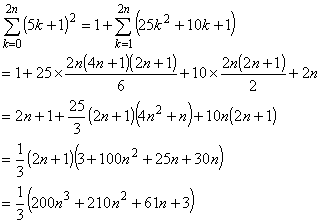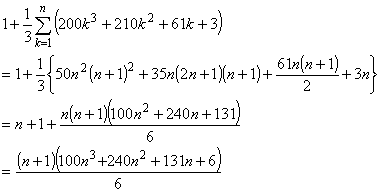| 問題
| n は自然数とする。
n × 100 円を，100 円玉，50 円玉，10 円玉，5 円玉，1 円玉に両替する方法は何通りあるか。
（大阪大学：改題）
|
|---|
少しずつ使う硬貨の金額を上げていって，見通しを立てていきます。
[A} すべて 1 円玉に両替する方法は，1 通り
以下，使わない硬貨があっても良いとして考えます。
[B] 5 円玉以下に両替するとき
10 × n 円を，5 円玉のみを使って支払う方法は，10 × n ÷ 5 = 2n
これと [A] より，10 × n 円を，5 円玉以下に両替する方法は 2n + 1 通りです。
[C] 10 円玉以下に両替するとき
同様に，10 × n 円を両替する方法を考えます。
10 × k 円を 5 円玉以下に両替する方法は，[B] より，2k + 1 （通り）
残りの金額は両替されません。
また，k = 0 のときは，すべて 10 円玉に両替する 1 通りがあります。
よって，10 × n 円を両替する支払う方法は，
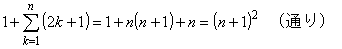かなりきれいになりましたね。
[D] 50 円玉を使える硬貨として追加したとき
100 × n 円を両替する方法を考えます。
100 × n ÷ 50 = 2n より，50 円玉は 0 枚から 2n 枚まで使えます。
50 × n = 10 × 5n より，
50 × k 円を 10 円玉以下に両替する方法は，(5k + 1)2通りですから，
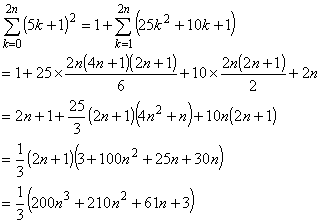
[E] 100円 円玉を使える硬貨として追加したとき
100 × n 円のうち，100 × k 円を [D] の方法で両替するとします。
残りはすべて 100 円玉に両替されるので，
|
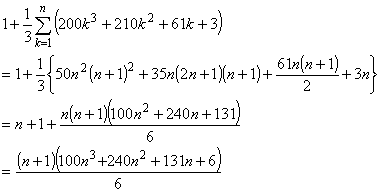