袋から球を取り出すと何色出る??
このお題はYSGさんより頂いた題材です。| 問題 | m色の球がn個ずつ袋に入っている。この中からk個を取り出すとき、 取り出される球は何色あることが期待できるか。 ただし、m≧kであるとする。 |
|
2種類のとき まず、小手調べに2種類のものを考えます。全体の個数は2n個です。この中からk個を取り出すので、全事象は2nCk通りです。 t色が取り出される確率の分子をptとする(以下同じ)と、 1色のみである場合はどちらの色を選ぶかの2通り、 取り出され方はそれぞれnCk通りずつありますから、 p1=2nCkとなります。 2色である事象は、「1色」のときの排反事象ですから、 p2=2nCk−2nCkです。 よって、2種類からk個とりだしたときに現れる色の数の期待値の分子は、 2nCk+2(2nCk−2nCk)=2(2nCk−nCk)ですから、 求める期待値は2−(2nCk/2nCk)となります。
3種類のとき 次に3種類です。 1種類、2種類となる事象は2種類のときと比べ、色の選び方だけが変わるので、 p1=3C1×nCk=3nCk p2=3C2×(2nCk−2nCk)=32nCk−6nCk 3種類のときは、やはり余事象を考えることにより、 p3=3nCk−3nCk−(32nCk−6nCk)=3nCk−32nCk+3nCk
以上より、期待値の分子は、 3−(32nCk/3nCk)となります。 ここで注目するべきなのは、nCkの項の総和がちょうど0になって消えてしまったことです。 これは果たして偶然なのかどうか、4種類の場合も調べてみましょう。 お気づきの方もいらっしゃると思いますが、 pnの値はお菓子のおまけが始めて全部揃う確率の分子に非常に良く似ていて、 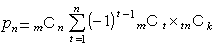 となります。 となります。
4種類のとき だんだんnCkや2nCkなどを書くのは面倒になってきたので、たとえば3種類のときのp3の値を、nCkの値から順に(3,−3,1)と書くことにして、 例えば(4,−4,3,2)であれば、4nCk−42nCk+33nCk+24nCkの値をさすことにします。 4種類のときは4次元になって、表にまとめると次のとおりになります。
さらに、期待値を計算するために、各pnの値にnを掛けた表を作り直し、合計を計算すると次のとおりになります。
この表から、4種類のときの期待値は4−(43nCk/4nCk)となります。 驚くことに、最後の2つ以外は全て0になって消えて行きそうではありませんか? 4種類までのところでm種類の期待値を推測すると、 m(1−(m-1)nCk/mnCk)であると推定できます。 証明は、二項定理を利用して微分していくと導くことができます。 もう一度4種類の場合をとりあげて、どんな等式が成り立っているのか確認してみます。 最終的なtnCkの係数は、 t=1 のとき 1*4C1*1C1−2*4C2*2C1+3*4C3*3C1−4*4C4*4C1=Σ{r*4Cr*rC1(-1)r-1} (r=1 to 4)
t=2 のとき
t=3 のとき
t=4 のとき 以上のことで解かるように、証明するべきは、 Σ{r*mCr*rCs(-1)r-1} (r=s to m)の値が、
[証明] s=mのとき s=m−1のとき その他のとき 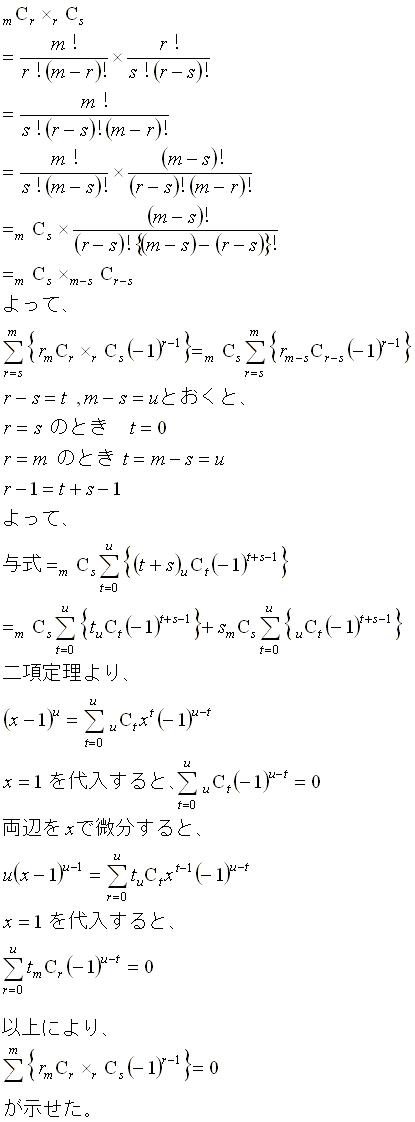 途中で(−1)の指数を置き換えないのは、−から始まっても、+から始まっても、 両辺に−1を掛ければ左辺が0になってしまうことを利用しています。 |
m色の球がn個ずつ袋に入っている。この中からk個を取り出すときの色の数の期待値計算機