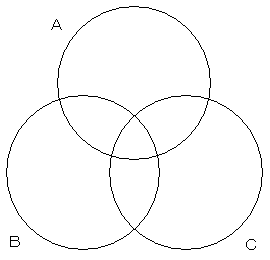集合の要素の個数

例えば，A = {1，2，3，4，5，6，7，8，9，10} のときは，n (A) = 10 です。
単位は不要です。

当たり前と言われればそれまでですが、次のことが成り立ちます。

性質	空集合 φ に対して，n (φ) = 0 全体集合 U の部分集合 A に対して，n (A) = n (U) ー n (A)

和集合の要素の個数について

2 つの有限集合 A，B に対して，n (A ∪ B) = n (A) + n (B) ー n (A ∩ B) が成り立つ。

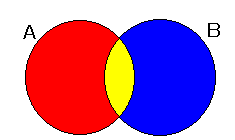
要素の個数の計算は，「すべての要素をちょうど 1 回ずつ」数えることが重要です。
共通部分が空集合でないとき，n (A) + n (B) を計算すると，共通部分を 2 度数えてしまいます。
このため、n (A ∩ B) を抜く必要が出ます。
共通部分が空集合であっても、上記の等式は成り立ちます。

例題 1	1 から 200 までの整数のうち，次のものの個数を求めよ。 (1) 2 の倍数 (2) 2 または 5 の倍数 (3) 2 の倍数でも 5 の倍数でもない整数

「1 から 200 まで」とは「1 以上 200 以下」のことです。
全体集合が 1 から始まるときは，全体を対象の数で割った商を求めるだけで構いません。

(1)	200 を 2 で割った商は 100 であるから，100 個
(2)	1 以上 200 以下の 5 の倍数は 40 個 　1 以上 200 以下の 10 の倍数は 20 個 以上より，100 + 40 - 20 = 120　(個)
(3)	(2)の補集合を指すので，ド・モルガンの法則より， 200 - 120 = 80　(個)

例題 2	100 から 200 までの整数のうち，次のものの個数を求めよ。 (1) 2 の倍数 (2) 2 または 5 の倍数 (3) 2 の倍数でも 5 の倍数でもない整数

100を含んで数えるので，全体は 101 個です。
確認ですが，例題 1 のうち，不要なものは「1 以上 99 以下」の整数なのです。(案外盲点のようです)

(1)	1 以上 99 以下の 2 の倍数は49 個あるから，100 - 49 = 51　(個)
(2)	1 以上 99 以下の 5 の倍数は 19 個あるから， 100 以上 200 以下の 5 の倍数は，40 - 19 = 21　(個) 1 以上 99 以下の 10 の倍数は 9 個あるから， 100 以上 200 以下の 10 の倍数は，20 - 9 = 11　(個) 以上より，51 + 21 - 11 = 61　(個) 単純に例題 1 の (2) を 2 で割ってはいけません。
(3)	(2)の補集合を指すので，101 - 61 = 40 (個)

3 つの有限集合 A，B に対して，次の等式が成り立つ。 n (A ∪ B ∪ C) = n (A) + n (B) ー n (A ∩ B) ー n (B ∩ C) ー n (C ∩ A) + n (A ∩B ∩ C)

言葉で説明するよりも，下のスライドで理解した方が早そうな気がします…

どこから拾ってきたか、忘れてしまいましたが、4 つの集合のベン図も描けるようです。

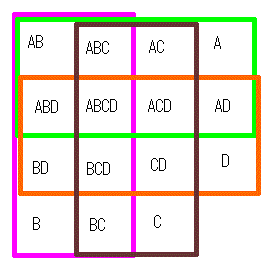
この図が参考になるかわかりませんが、共通部分が奇数個あるときは加える方向、
共通部分が偶数個あるときは減ずる方向になります。この法則を交代和と呼ぶことがあります。