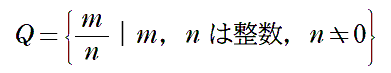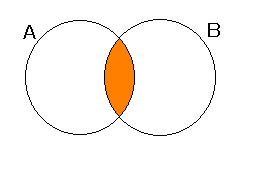| 定義
| いくつかのものを,ひとまとめにしたものを集合という。
また,集合 A に対して,a というものが A の中に属するとき,
a は集合 A の要素である,といい,記号で a ∈ A と書く。
さらに,b というものが A に属さないとき,記号で b 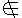 A と書く。 A と書く。
|
例:東京都民全員の集合を A,神奈川県民全員の集合を B とします。
a さんが東京都民のときは,a ∈ A であり,a 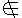 B です。 B です。
集合の表し方
どの方法も,中カッコ{}で挟まなくてはいけまん。
集合 A を,1 桁の自然数全体の集合とするとき,次の方法があります。
| (1) | すべての要素を列挙する方法
A = {1,2,3,4,5,6,7,8,9,10}
| | (2) | 要素の条件を述べる方法
A = { x | 1 ≦ x ≦ 10,x は整数}
{式 | 式の属性(範囲)}と表します。
例:B = { 2n + 1 | n は整数,1 ≦ n ≦ 10}
1 ≦ n ≦ 10 を満たす整数を,2n + 1 に代入します。よって,集合 B を列挙すると,
B = {3,5,7,9,11,13,15,17,19,21} となります。
この表し方は,列挙することができない集合を表すときに有効です。
例:C = { x | x は有理数,1 ≦ x ≦ 10}
集合 C の要素には 1.35,5/3 などがあり,列挙不可能です。
例:D = { x | x は整数,1 ≦ x ≦ 100}
列挙できてもそれが面倒なときにも便利ですね。 |
規則性がつかめれば D = {1,2,3,4,…,100}と中略してもかまいません。
蛇足ですが,有理数全体の集合を Q とすると,集合 Q を条件を述べる方法で書くと次のようになります。
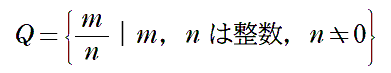
A,B,D のように,何個あるか分かる集合を,有限集合,
C のように,要素の個数が無数にある集合を,無限集合といいます。
例:E = { x | x は正の奇数}
これも,キリがないので無限集合の 1 つです。
| 定義
| 集合 A のすべての要素が集合 B の要素であるとき,
集合 A は集合 B の部分集合である,といい,記号で A ⊂ B と書く。
また,集合 A と集合 B の要素が完全に一致するとき,
集合 A と集合 B は等しい,といい,記号で A = B と書く。
|
「∈」と「⊂」の違い
相手が要素(これ以上分けることができないもの)に対しては「∈」,
相手も集合であるときが「⊂」です。
例えば,(会津若松市)⊂(福島県)という感じです。
「会津若松市民全体」は,まだ集合ですから・・・
| 定義
| 2 つの集合 A,B に対して,
A にも B にも属する要素全体の集合を積集合(共通部分)といい,記号で A ∩ B と書き,
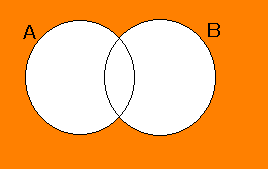
A または B の少なくとも一方に属する要素全体の集合を和集合といい,記号で A ∪ B と書く。
|
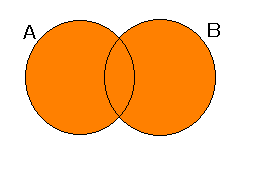
イメージは下の図のとおりです。
| A ∩ B | A ∪ B
|
|---|
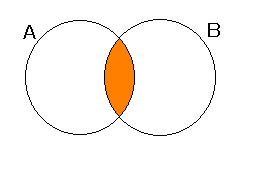 | 
|
|---|
例: A = {1,3,5},B = {2,3,6} のとき,A ∩ B ={3},A ∪ B = {1,2,3,5,6}
和集合について,共通部分があっても,上の例のように,1 度しか書かない約束になっています。
また, 2 つの集合はいつも共通部分があるとは言えません。(例:郡山市と,福島市)
つまり,要素のない集合も,ありえるのです。
要素のない集合を空集合といい,慣例的に記号でφと表します。
例: A = {1,3,5},B = {2,4,6} のとき,A ∩ B = φ
| 定義
| 集合 A に対して,A に属さない要素の集合を,A の補集合といい,記号で A と書く。
|
これだけだと,どんな A に対しても A の補集合は無限集合となってしまいます。
また,一般的にも,数学の世界では,ある集合の中に「ふたをして」話を進めることがほとんどです。
| 定義
| ある集合の中でしか要素を考えないとき,その要素全体の集合を,全体集合 という。
|
Universal Set の頭文字から,慣例的に U と表します。
U を全体集合としたとき,U の部分集合 A に対して,次のことが成り立ちます。
A ∩ A = φ, A ∪ A = U,集合 A の補集合は A
Aのイメージ図は下のとおりです。
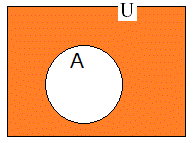
A,B が U の部分集合のとき, A が伴うと少し難しくなるようです。
| 記号: | 意味
|
|---|
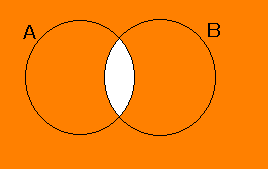
| A ∩ B: | A でないが B である。
| | A ∪ B: | A でない,または B である。
| | A ∩ B: | A でも B でもない。
| | A ∪ B: | A でない,または B でない。
|
特に,∪のほうは言われもピンと来ない人が多い印象があります。
下の集合や記号の上にあるボタンをいろいろ押して、変化を観察しましょう。
上のボタンをいろいろ押しているとド・モルガンの法則が成り立つことも分かります。
3 つ以上の集合の共通部分や和集合を考えるときは,カッコをつけないと意味不明になります。
例えば A ∩ B ∪ C は意味不明(このような表記をすること自体が誤り)です。
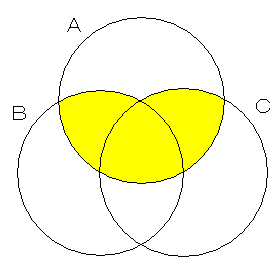
カッコのつけ方を変えると,次のように,塗られる場所が異なってしまうからです。
| (A ∩ B) ∪ C | A ∩ (B ∪ C)
|
|---|
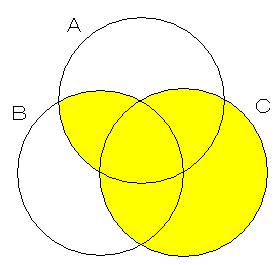 | 
|
ただし,3 つの集合の共通部分 A ∩ B ∩ C と,和集合 A ∪ B ∪ C は,誤解を生まないので,カッコが不要です。
集合の要素の個数
Back
|  A と書く。
A と書く。