等差数列の和に関する問題について

等差数列の和の公式は２つありました(証明はこちらです)が、
２つめの公式を使わずに切り抜ける方法を説明します。

例 1　初項 3，公差 4，項数 20 の等差数列の和を求めよ。
末項を l とすると，l = 3 + (20 - 1)× 4 = 79 より，求める和は，

20 × (3 + 79) = 820
2
少しだけ、手間はかかりますが、あまり変わらないようです。

例 2　5 から 31 までの奇数の和 5 + 7 + 9 + … + 31 を求めよ。
等差数列の和に必須なのは，初項と項数です。
項数を n とすると，公差は 2，末項は 31 であることから，5 + 2(n - 1) = 31
これを解くと，n = 14
ここまで揃えば，上に紹介した公式の方が早いですね。求める和は，
14 × (5 + 31) = 252
2

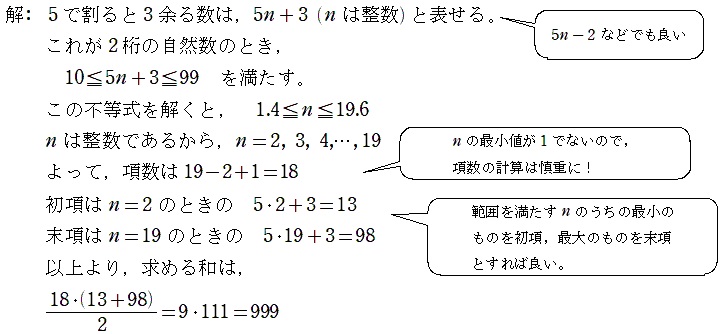
例 3　2 桁の自然数のうち，5 で割ると 3 余る数の和を求めよ。
この例であれば、勘で初項と末項が求まる人も居るでしょう。
ここでは，その勘が働かなかった場合の解法を紹介します。

例 4　初項 3，公差 2 の等差数列の，初項から第 n 項までの和が 63 であるとき， n の値を求めよ。

条件次第では，2 つとも答えになる場合もあります。その条件を考えるのも，面白いと思います。