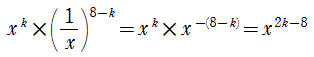n 個から r 個とる組合せは,nCr です。
組合せの基本で述べたことをもとに,定理を紹介します。
|
二項定理 (a + b)n の展開式における,arbn−r の項の係数は,nCr
|
まず,(a + b)4 の展開式における,a2b2 の項の係数を考えてみましょう。
理解のポイントは,本当に展開してしまうのではなく,次のように並べて考えることです。
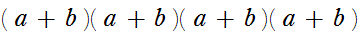
このスライドの順に,aabb,abab,abba,baab,baba,bbaa と出現します。
積の順をアルファベット順に並べると,すべて a2b2 となります。
| この並べ方は, | 4! | つまり,4C2 通りです。
| | 2!2!
|
一般にも,(a + b) をn 回掛けたとき,a を r 回選ぶと,残りの n−r 回は自動的に b が選ばれるので,
(a + b)n の展開式における,arbn−r の項の係数は,nCr となります。
このことから,nCr は二項係数と呼ばれることがあります。
パスカルの三角形
二項係数を並べると,次のようになります(好きなだけ増やすことができます)。
左(右)から2番目の数が,何段目であるかを示してます。
| これより,(a + b)n = | n
Σ
r = 0nCr arbn−r
| |
ちなみに,Σの記号は,「r = 0 から,r = n となるまで足しなさい」という命令記号です。
さらにこの図を眺めていると,両端以外は,その上の数の和になっていることに気づくと思います。このことから,
nCr + nCr + 1 = n + 1Cr + 1 も成り立ちます。
二項定理のその他の定理やその数式的な深入りは別ページで扱うことにして,
ここでは二項定理の基本的な問題を紹介します。
|
例題 1 (a + b)7 の展開式における,a3b4 の項の係数を求めよ。
|
二項定理より,7C3 = 35
くどいようですが,残りの 4 回は自動的に b を選んでいるので,考える必要はありません。
|
例題 2 (a + b + c)7 の展開式における,a2b3c2 の項の係数を求めよ。
|
カッコの中の項が 3 つ以上になったときは,同じ文字を含む順列の考え方が威力を発揮します。
つまり,aabbbcc の並べ方と等しく,実は私も,「数字を使い切る」ほうが好きなので,次のように計算します。
| 7! | = | 7・6・5・4 | = 210
| | 2!3!2! | 2・2
|
一般にも次の定理が成り立ちます。
|
多項定理 (a + b + c)n の展開式における,ap bq cr (ただし,p + q + r = n)の項の係数は
|
この定理は,カッコの中が 4 項以上であっても,同様に成り立ちます。
|
例題 3 | (2a −b)7 の展開式における,次の項の係数をそれぞれ求めよ。
(1) a3 b4
(2) a2 b5
|
2a = x,−b = y とおいて,例題 1 と同様に考えてみます。
| (1) | (x + y)7 の展開式における,x3 y4 の係数は,7C3 = 35
ここで,x3 y4 = (2a)3 (−b)4 = 8a3 b4 ですから,求める項の係数は,
35 × 8 = 280 となります。
つまり,考える項の対象の係数が 1 でないときは,その係数を連動させる必要が出ます。
| | (2) | (1) の考え方をもとに一気に計算式を作ると,
7C2 × 22 × (-1)5 = -84
忘れ物になりやすい、「各項の係数を連動させる」ことを先に計算しても良いでしょう。
|
|
例題 4 | (2a + b − c)7 の展開式における,a2 b2 c3 の項の係数を求めよ。
|
例題 2,3 の融合問題です。これらの考え方より,求める係数は,
| 7! | × 22 × 12× (-1)3 = -840
| | 2!2!3!
|
|
例題 5 | 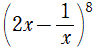 の展開式における,次の項の係数をそれぞれ求めよ。 の展開式における,次の項の係数をそれぞれ求めよ。
(1) x2
(2) 定数項
|
指数法則を理解した後でないと,難しいかもしれませんが…
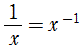 であることを用い,「2x」を k 回使ったときの,x の指数を仮に求めておきます。 であることを用い,「2x」を k 回使ったときの,x の指数を仮に求めておきます。
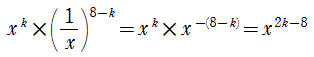
| (1) | 2k −8 = 2 を解くと,k = 5 ですから,求める係数は,
8C5 × 25 × (−1)3 = −1792
| | (2) | 突然定数項と言われると驚くかもしれませんが,このときは指数が 0 のときと理解してください。
2k −8 = 0 を解くと,k = 4 ですから,求める係数は,
8C4 × 24 × (−1)4 = 1120
|

| 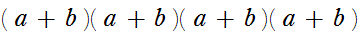
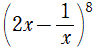 の展開式における,次の項の係数をそれぞれ求めよ。
の展開式における,次の項の係数をそれぞれ求めよ。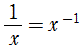 であることを用い,「2x」を k 回使ったときの,x の指数を仮に求めておきます。
であることを用い,「2x」を k 回使ったときの,x の指数を仮に求めておきます。