組合せについて

定義

異なる(区別のつく) n 個のものから，ちょうど r 個選ぶ方法を，
n 個から r 個とる組合せといい，記号で nCr と表す。
＊ C は Combination の頭文字です。

例えば 6 人の生徒から，A，B，C の 3 人を選ぶとき，次のものはすべて同じとみなします。

ABC　ACB　BAC　BCA　CAB　CBA

　上のように，並べ方を考慮しません。
ここで，nCr = k とおくと，選ばれた k 個のそれぞれに，r! 通りの並べ方があります。
また，並んだ後のものは， n 個から r 個とる順列 ですから，
　k×r! = nPr　が成り立つので，次の公式を得ます。
公式 1　　nCr = nPr
r!
これより，6 人の生徒から 3 人を選ぶ方法は，次の図のように計算されます。
r を 2 度使うのも特徴です。
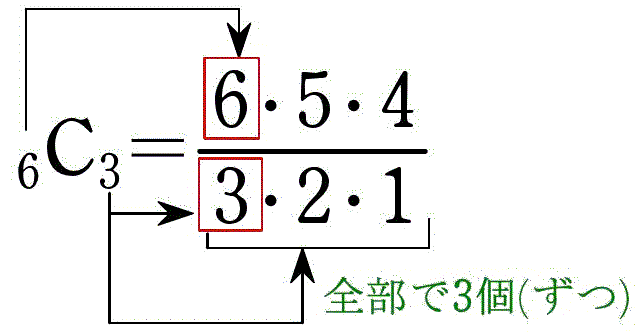これより，6 人の生徒から 3 人を選ぶ方法は，6C3 = 20 （通り）
まとめ　「選ぶだけ」が C ，「選んで並べる」が P

また，公式 1 に　nPr = n!　を代入すると，次の公式を得ます。
(n−r)!
公式 2　　nCr = n!
r!(n−r)!

公式 2 は二項定理に関する様々な等式で用いられる重要な公式です。
さらに，公式 3 の r の代わりに n−r を代入すると，n−(n−r) = rより，次の公式を得ます。

公式 3　　nCr = nCn−r

この式だけでは重要度が理解できないと思うので，「6 文字から 4 文字を選ぶ」の 1 例で考えてみます。

A　B　C　D 　E　F

このとき，4 文字（ABCD）を選ぶより，2 文字（EF）を取り除いたほうが早い、ということです。
つまり，6C4 = 6C2　が成り立ちます。

さらに，公式 2 に r = 0 を代入すると，定義より 0! = 1 ですから，次の値も求まります。
公式 4　　nCn = nC0 = 1

このほかにも，多くの公式がありますが，それはパスカルの三角形(二項定理)に送ることにします。
＊　nCr　の計算機（半角の数字を入力してください。）

C 　＝

Back