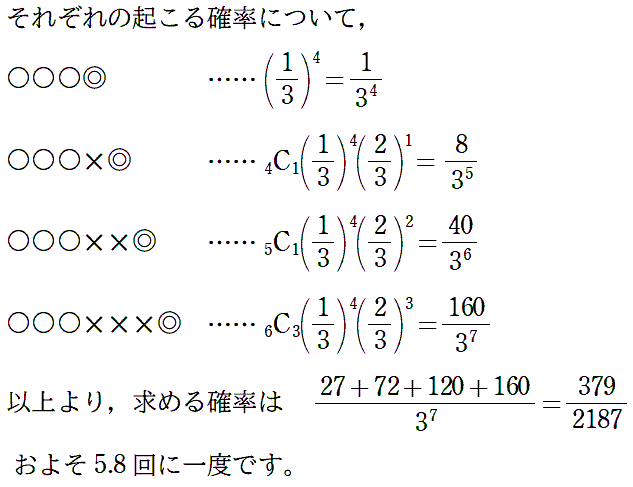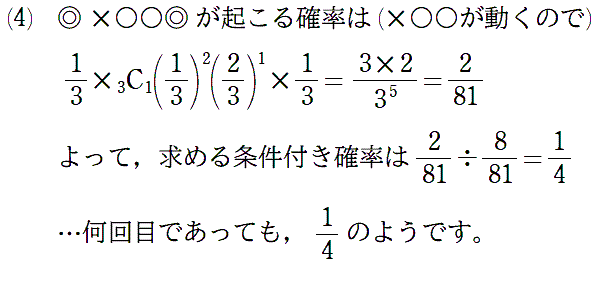日本シリーズ的な確率

例題 1 　さいころ 1 個を何度か投げる。
2 以下の目が出ると A さんに 1 点，3 以上の目が出ると B さんに 1 点を与える。
A，B のいずれかが 4 点になった時点でその人の優勝としてさいころ投げを終える。

(1)　5 回目に A さんが優勝する確率を求めよ。
(2)　5 回目に B さんが 3 点目を与えられる確率を求めよ。
(3)　ちょうど 6 回で優勝が決まる確率を求めよ。
(4)　A さんが優勝する確率を求めよ。
(5)　5 回目に A さんが優勝したとき，1 回目は A さんが得点していた条件付き確率を求めよ。
(6)　さいころを投げる回数の期待値を求めよ。

設定を「2 チームが試合をして，先に 4 勝したチームが優勝」に置き換えると，
「日本シリーズ」のようになるので，私はこれを「日本シリーズ系」と呼んでいます。

この問題も反復試行の問題の 1 種ですが，ある条件を満たすと試行が終わることが，大きな特徴です。
例えば裏を×，表を〇として並べ替えたとき，〇〇〇〇×，のようなことは (4 回目で試行が終わっているので)起こり得ません。

Point 試行が終わるときを◎などと別の記号にすると，◎は動けない

どういうことなのか，上の例題で説明しましょう。

(1)
(2)
(3)
(4)
(5)
(6)

くだらない計算機・・・

A さんと B さんが試合をし，先に勝したほうを優勝とする。
1 試合あたりに A さんが勝つ確率は 小数でも分数(1/3 など)でも OK

Ａさんが優勝する確率はおよそ？？？回に１度
試合数の期待値は？？？試合

＊確率設定の都合上，分数での表示は行っておりません。悪しからず…

目次へ