最短経路の場合の数について

例題 1　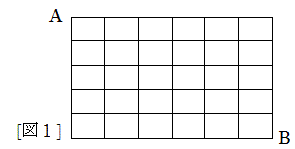 図 1 のような街路をもつ町がある。A 地点から B 地点へ最短経路で向かうとき，その道順は何通りあるか。

　カーソルキーで，「→」と「↓」だけを使って B 地点へ向かう方法と捉えます。
どの経路であっても，→を 6 回，↓を 5 回押すと，B 地点に到着します。
よって，→ 6 個と↓ 5 個の並べ方と等しくなるので，求める場合の数は，

11!	=	11・10・9・8・7	= 462　(通り)
6!5!		5・4・3・2・1

この問題を，次の手法で教わった人がいるかもしれません。

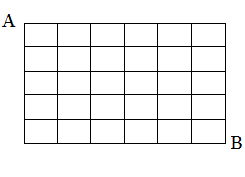
原理が分からなくても、小学生でもできそうな解法といえますが，1 度でも足し算を間違えると終わります…
見方を変えて，A を中心に，時計回りに 45°回転すると，パスカルの三角形となります。
この加えていく解法，実は，パスカルの三角形の原理に従っているだけなのです。

例題 2　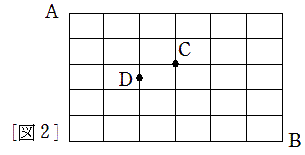 図 2 のような街路をもつ町がある。 A 地点から B 地点へ最短経路で向かうとき，次のような道順はそれぞれ何通りあるか。 (1)　C を通る (2)　C を通らない (3)　D を通る

(1)	A から C までと，C から B までの道順に分けて考えます。 A から C までの最短経路は， 5! = 10　(通り) 2!3! C から B までの最短経路は， 6! = 20　(通り) 3!3! 以上のことがらは独立しているから，10 × 20 = 200　(通り)
(2)	A から B まで向かう方法は，例題 1 より，462 通り このうち，C を通るものは，(1) より，200 通りある。 よって，C を通らない最短経路は，462 − 200 = 262 (通り)
(3)	D が交差点でない場合も，(2) と同様に考えます。 A から「D の入り口」までの最短経路は， 4! = 6　(通り) 2!2! 「D の出口」C から B までの最短経路は， 6! = 15　(通り) 2!4! 以上より，D を通る方法は，6 × 15 = 90　(通り) 例題 3　 図 3 のような街路をもつ町がある。 A 地点から B 地点へ最短経路で向かう方法は何通りあるか。 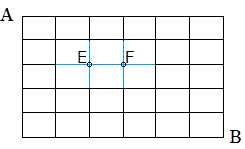このように，最初から穴が開いているときも，右図のように条件なしの街路を作ってしまいます。 条件なしで A から B へ向かう方法は， 11! = 462　(通り) 6!5! このうち，E を通過する方法は， 4! × 7! = 210　(通り) 2!2! 4!3! Fを通過する方法は， 5! × 6! = 200　(通り) 3!2! 3!3! E，F 両方を通過する方法は， 4! × 6! = 120　(通り) 2!2! 3!3! 以上より，E まはた F を通過する方法は，210 + 200 − 120 = 290　(通り) よって，E も F も通過しない方法は，462 − 290 = 172　(通り) 「例題 3 の(2) から D を通過する場合を除く」ことに気づいた人はすごいと思います。