分散と標準偏差について
|
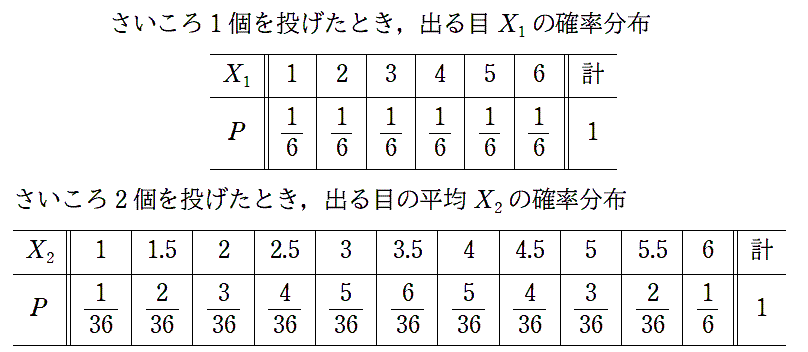
期待値のところで取り上げたとおり、 1つのさいころを投げたときに出る目の期待値は 3.5 です。 2つのさいころを投げたときに出る目の平均の期待値も、3.5 です。 しかし、この2つを同じと扱ってよいかどうかには、疑問が残ると思います。 まずは、2つの確率分布を比べてみましょう。
|
|
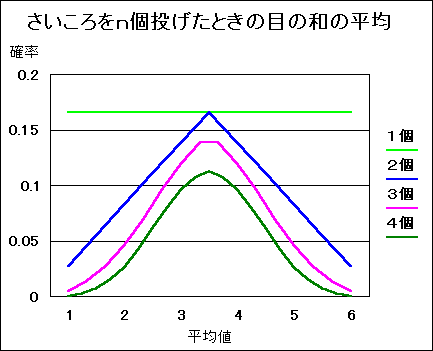
見た感じでも、明らかに同じと扱えないことが分かると思います。 さらに3個、4個と増やしてみて比べてみると、次の図のようになります。 |
|
だんだんと、「釣鐘型」に近づいていくことが分かると思います。明らかに「ばらつき方」が異なっていますね。 そこで、平均値 からの差の2乗を考えてみることにします。 |
定義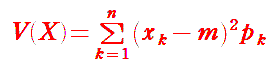
|
|
V は Valiance(相違)の頭文字です。xk−m を偏差と言います。 偏差の平均は必ず 0 になってしまうので,違いが顕著になるように 2 乗をする,と解釈しています。 ただし、目の和の平均の単位を「点」とすると、分散の単位は「点2」となり、いかにも変です。 そこで、単位を揃えるために、分散の正の平方根を考えます。これを X の標準偏差と呼び、σ(X)と書くことにします。 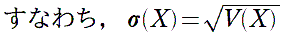 σは「シグマ(Σ)」の小文字です。標準偏差が小さければ小さいほど、「分布は平均付近に密集している」と言えます。 ここで,さいころ 1 個を投げたときに出る目 X1 の分散および標準偏差を求めてみましょう。 紙の上で計算するときの工夫として,確率分布の表を少し改変します。 |
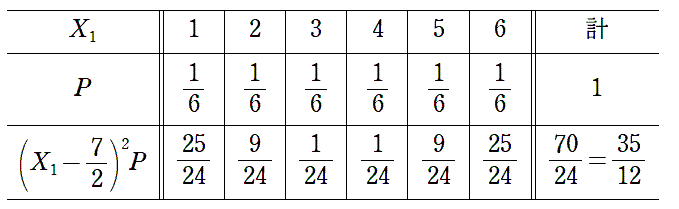
|
3段目の計算をもっと要領よく計算したいので,便利な公式を紹介します。
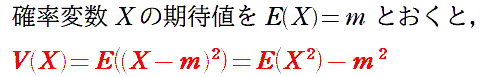 公式の覚え方は(2乗の平均)−(平均の2乗)です。証明はこちら
さいころ 1 個を投げたときに出る目 X1 の分散を紙で計算したいときには、 |
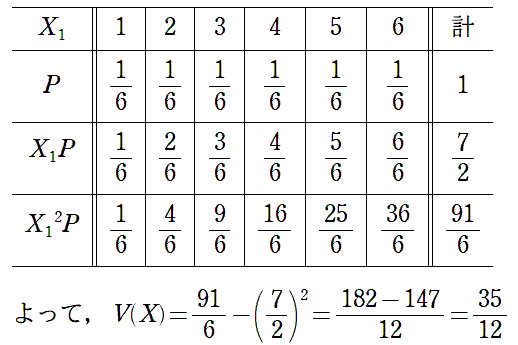
|
・・・あまり変わり映えしませんが、期待値もこれから求めなくてはいけない場合には後者が断然有利で, こちらの方法では期待値と分散を同時に求めることができます。この方法で 2 つのさいころを 同時に投げたときに出る目の和の平均値 X2 の期待値と分散を求めてみます。  そして、かなり大変になってきました。もっと楽にできないか、考えてみます。 また,2 つの確率変数 X,Y が互いに独立ならば、次の公式が成り立ちます。 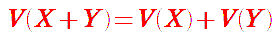 証明はこちら 証明はこちらまた,実数の定数 a,b に対して,次のことも成り立ちます。 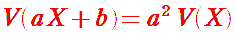 証明はこちら 証明はこちら
|
偏差値の意味
一般に使われる偏差値は、次のような公式で与えられます。
|
標準化すると必ず平均値が 0,標準偏差が 1 になります。 上で登場した公式を駆使するとすぐに導けますが、 標準化についての詳しい話は将来「正規分布」で扱いたいといます。  標準化したのち10倍しているのは,違いがはっきりわかるようにするためと思われます。 平均値が 1 のときの偏差値がどんどん下がり,6 のときの偏差値がどんどん上がるのは, それだけ分布が広くなっている(それぞれ集団から離れていっている)ことを意味します。 蛇足ですが、n=60 のとき,x=1の偏差値は -0.7 になります。 空想的すぎますが、平均点が極端に高い試験で 0 点などをとってしまうと, さすがに偏差値もマイナスになるようです・・・ |
登場した公式の証明集
| (1) | 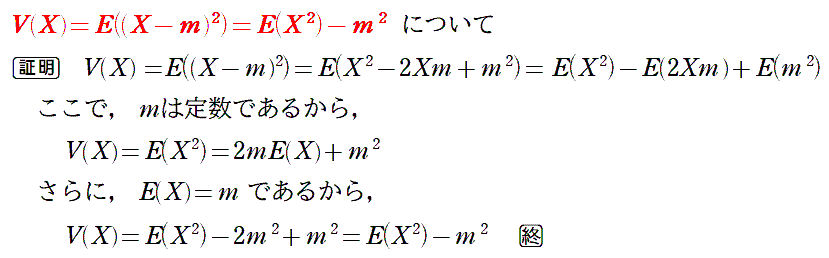 |
| (2) | 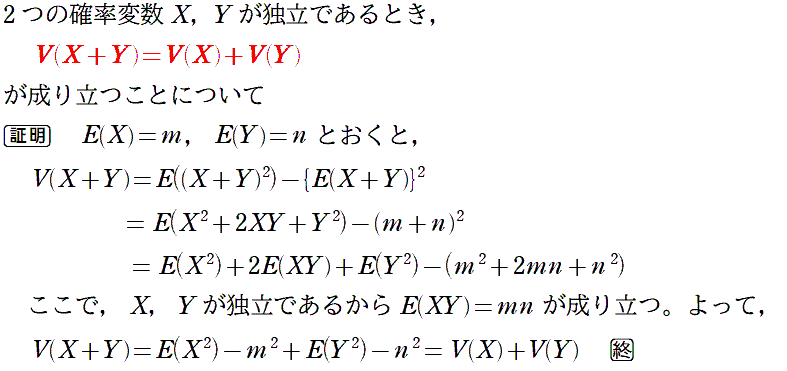 |
| (3) | 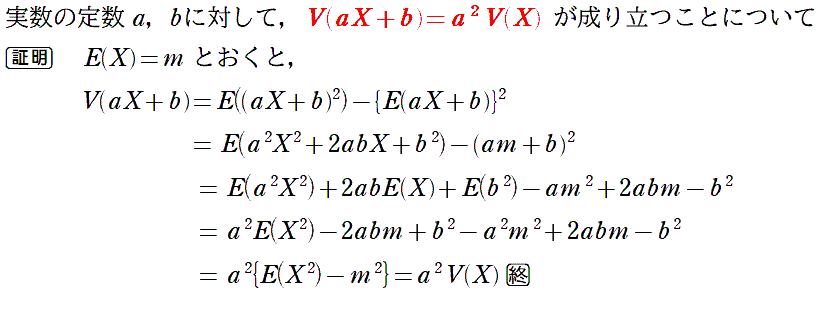 |
正規分布について(多分やります)
母平均について(気が向いたらやります)
Back
