ビンゴゲームについて

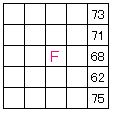
数は関係ないので、最も右側の列しか数字が入ってません（笑）
ついでですから、一般にありがちな真ん中はＦＲＥＥであるとしましょう。
ルール；自分のカードには、１〜７５の数が１つずつ任意に書いてある。
袋の中から数字の書いてある球を１枚ずつ取り出す（元に戻さない）
取り出された球の数字が自分のカードにあれば、それを塗りつぶす。
塗りつぶされた領域が縦横斜めに５つ連続すれば当たりとする。
４回でBINGOとなる確率
もっとも考えやすいのが、この「ストレートで当たる」確率です。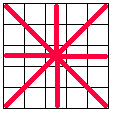
図１
まず，３つを同時に取り出したとき，それが図１の直線のうちの１つの上に並ぶことが条件です。
直線の選び方は４通り、空きマスの選び方が４通りあるので、
確率は16×（１／75Ｃ3）×(１/72)＝2/607725です。
およそ３１万回に１回の割合です。

５回目まででBINGOとなる確率


４回のときと同様、直前までの４回は一度に取り出したとみなして良いので、
全事象は75Ｃ4×71通りです。
直線は全部で１２本引け、そのうちの４本がFREEマスを通る直線です。（図１）
以降、FREEマスを通る直線を直線Ａ、通らない直線を直線Ｂとします。
Ａ． 直線ＡでBINGOになるとき
　１〜４回までの１回が外れで、残り４回がその直線上に来る。
　直線の選び方は４通り、外れの数の選び方は７１通り。
　当たりになるまでの数の並べ方は４×４！通りなので、
　４×71×４×４！＝142×８×４！通り

Ｂ．直線ＢでBINGOになるとき（８通り）
　全てその直線上の数が当たるので、５！通り。
　よって、８×５！＝５×８×４！通り。

　ＡＢより、（５＋142）×８×４！＝147*８*４！＝４９×３×８×４！
　よって求める確率は(49*３*８*４！)／(75*74*73*72*71)＝196／14382825
　以上より、５回以内にビンゴとなる確率は、ちょうど４回でビンゴになる確率を加えて、
　2/607725＋196／14382825＝(142＋588)/43148475＝2/118215
　およそ５万９千回に１度の割合です。

検証；４回以内で当たっている確率を最初から計算できないか？
順列で考えると厄介なので，一度に５個とった場合、それが１直線を選んでいる場合の数、
つまり、本当は５回目で初めて外れる場合も、参加させてみます。
全事象は75Ｃ5＝17259390通りとなります。
Ａ．直線Ａが選ばれるとき
　直線の選び方は４通り、他の数の選び方は７１通り。
　以上より、４×71＝284通り Ｂ．直線Ｂが選ばれるとき
　直線の選び方は８通りある。
よって，(284+8)/17259390＝2/118215となり、お見事、同じになりました。

６回目までで当たりとなる確率


５回の一致は偶然かどうか調べたいので、一旦ちょうど６回で当たる確率を求めてみます。
直前までの５回は１度に取り出したとみなしてよいので、
全事象は75Ｃ5×70通り。 この場合もダブルリーチになることはないので、先に直線を決めます。
Ａ． 直線ＡでBINGOになるとき
５回のうち、２個がハズレで３個がその直線になるので、
４×71Ｃ2×4Ｃ3＝39760通り
Ｂ．直線ＢでBINGOになるとき
５回のうち、１個がハズレで４個がその直線上に来るので、
８×70×５＝2800
ＡＢより、ちょうど６回で当たる確率は(39760＋2800)/1,208,157,300＝304/8,629,695
これに５回目以下でビンゴになる確率を加えると、
2/118215＋304/8,629,695＝2*(73+152)/8629695＝10/191,771 およそ１万９千回に１度の割合です。

これも同様に１度に６個とって直線が選ばれている確率から考えてみましょう。
全事象は75Ｃ6＝201,359,550通り
直線Ａが選ばれるときは、４×71Ｃ2＝9,940
直線Ｂが選ばれるときは、８×70＝560通り
以上より，(9,940＋560)／201,359,550＝10/191,771となり、やっぱりお見事、となります。

７回目までで当たりとなる確率


一度に７個とって良く、全事象は75Ｃ7
直線Ａが選ばれるときは，４×71Ｃ3＝228,620
直線Ｂが選ばれるときは，８×70Ｃ2＝19,320
以上より，(228,620＋19,320)／75Ｃ7＝1,078/8,629,695
およそ８千回に１度の割合です。
８回目以降について

目次へ