ビンゴゲームについて
8回以内でBINGOとなる確率のベタ解答編
|
FREEを通る縦(横)の直線をA1直線(2本) FREEを通る斜めの直線をA2直線(2本) A1直線とA2直線をまとめてA直線 その他の直線をB直線(8本)とします。 7回以下でビンゴになる確率は,(4×71Cn-4+8×70Cn-5)/75Cnなのですが、 この式にn≧45を代入すると1を超えてしまいます。 逆に7回以下で成立するのは「同時に2つ以上ののビンゴが成立しない」からなのです。
|
8回以内にBINGOとなる確率参考のために、次の2つの図を用意します。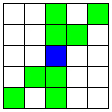 図1 図1 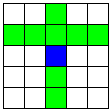 図2 図2まず、ちょうど8回で上がる確率を考えます。そのため、7個は一度に取ったものとします。 よって、ここでの全事象は75C7×68通りとなります。 A1直線でBINGOになるとき A2直線でBINGOになるとき B直線でBINGOになるとき よって、8×5×(70C3−3)=2189480通り。 BINGOになったときに2つの直線を同時に選ぶとき 以上より、ちょうど8回でBINGOになる確率は (7773024+7772992+2189480+24)/(75C7×68)=147796/1124736915 8回以内でBINGOになる確率は147796/1124736915+1078/8629695=864886/3374210745 およそ3900回に1度の割合です。 さて、今は直接求めて見ましたが、8個を一度に取ったときに、一本以上の直線を選んでいる確率 (4×71C4+8×70C3−30)/75C8と等しくなります。 30を引くのは、次の2つを重複して数えているからです。 (i-a) 2つのA直線を選ぶとき (4C2=6) (i-b) 交わるA直線とB直線を選ぶとき (8×3=24) 9回以内にビンゴになる確率も、同様に重複の分だけ引けばよいことになります。
9回以内にBINGOとなる確率8回以内のときと同様に、何も考えずに計算すると、分子は4×71C5+8×70C4となりますが、 次のものが重複して数えています。 (i-a,b)と1回はずれ(30×67C1) (ii-a) 平行なA直線とB直線 (2×4=8) (ii-b) 交わる2本のB直線 (4×4=16) よって、9回以内にBINGOになる確率は、 (4×71C5+8×70C4−2034)/75C9=9902127/20932603696 およそ2100回に一度になります。 |
|
さて、以下のすべての場合において、上の(i-a,b),(ii-a,b)の重複は必ず引くことになります。 そのため、先にn個塗ったときに初めて現れる重複をチェックしていくことにします。 |
nマスを塗って初めて現れる重複について(17≦n≦24)
ビンゴの確率計算について