| n | 例 | 説明 | 組合せ | 本数 | 合計
(dk) |
|---|
| 8 | 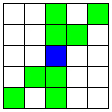 | 2本のA直線 | 6 | 2 | -30 |
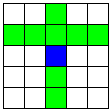 | B直線と、それに交わるA直線 | 24 | 2 |
| 9 | 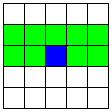 | A2直線と、それに平行なB直線 | 8 | 2 | -24 |
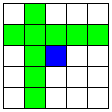 | 交わる2本のB直線 | 16 | 2 |
| 10 | 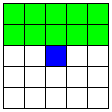 | 2本の平行なB直線 | 12 | 2 | -12 |
| 11 | 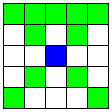 | B直線と、それに交わる2本のA直線 | 24 | 3 | 48 |
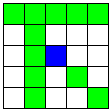 | A1直線と、交わる2本のB直線
ただし、B直線の交点はA1直線上でない | 24 | 3 |
| 12 |  | 3本のA直線 | 4 | 3 | 104 |
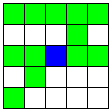 | A2直線とそれに平行なB直線、
その2本と交わるA直線またはB直線 | 56 | 3 |
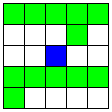 | 平行な2本のB直線と、それに交わるA直線 | 36 | 3 |
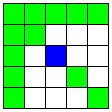 | 1つのMマスで交わる3直線 | 8 | 3 |
| 13 | 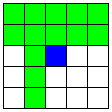 | 交わる2本のB直線、
3本目のB直線 | 48 | 3 | 40 |
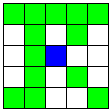 | 2本のA2直線と、Nマスで交わる2本のB直線 | 8 | 4 |
| 14 | 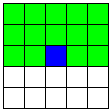 | A2直線と、それに平行な2つのB直線 | 12 | 3 | -136 |
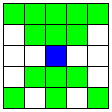 | B直線と、それに交わる3本のA直線 | 8 | 4 |
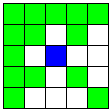 | 2本のA2直線と、Mマスで交わる2本のB直線 | 8 | 4 |
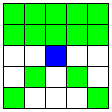 | 平行な2本のB直線と、
それに交わる2本のA直線 | 36 | 4 |
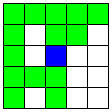 | A1直線とA2直線を1本ずつ、
選ばれたA1上でないMマスまたは
Nマス上で交わるB直線 | 48 | 4 |
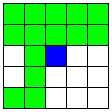 | A1直線と、平行な2つのB直線、
3直線に3点で交わるB直線 | 48 | 4 |
| 15 | 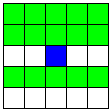 | 3本の平行なB直線 | 8 | 3 | -136 |
 | A1直線と、それに平行なB直線
残り3本のA直線のうちの2つ | 24 | 4 |
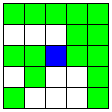 | Mマスで交わる3本の直線と、A2直線 | 16 | 4 |
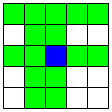 | 2本のA2直線と、交わるB直線 | 16 | 4 |
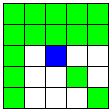 | 一つのMマス上で交わる3直線と、B直線 | 48 | 4 |
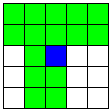 | A2直線と、それに平行なB直線、
A2直線と交わる2本のB直線 | 48 | 4 |
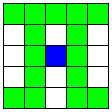 | 2本のA1直線と1本のB直線。
選ばれたB直線とNマスで交わる2本のB直線 | 8 | 5 |
| 16 | 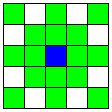 | 4本のA直線 | 1 | 4 | -27 |
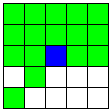 | A2直線と、それに平行な2つのB直線と、
残ったA直線の1つ | 36 | 4 |
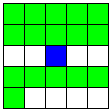 | 3本の平行なB直線と、
それに交わるA直線 | 24 | 4 |
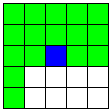 | A2直線と、それに平行な2つのB直線
それに交わる1つのB直線 | 48 | 4 |
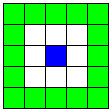 | 4本のB1直線
または
4本のB2直線 | 2 | 4 |
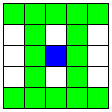 | 平行なB1直線と、それに交わる2つのB2直線
自動的に2本のA1直線を追加する。 | 0 | 4〜6 |
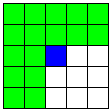 | まずA1直線を1つ選び、Mマスを4個使う。
5個目のMマスで交わるB1直線、
6個目のMマスで交わるB2直線
(見た目には4つのB直線とも解釈できるため、4重複とも5重複とも解釈できる)
| 0 | 4or5 |
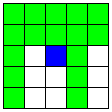 | 3本のB1直線と、選ばれなかったB1直線に平行なB2直線
(上記説明のB1とB2は交換可)
または
隣り合うB直線と、それに交わり、
かつ隣り合わないB1直線とB2直線 | 24 | 4 |
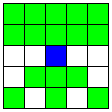 | 2本の平行なB直線と、それに交わる3本のA直線 | 12 | 5 |
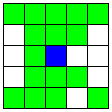 | 2本のA1直線
Nマスで交わるB直線、
A2直線 | 16 | 5 |
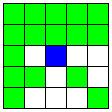 | 2本のA1直線(1通り)
Mマスで交わる2本のB直線(8通り)
2マスだけをつぶすような3本目のB直線(4通り) | 32 | 5 |
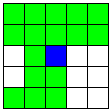 | 1本のA2直線、それに交わる2本のB直線とA1直線
A2に平行で、他の直線と3回交わるB直線 | 48 | 5 |
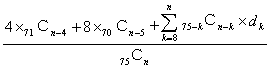 となります。
となります。 マスの名称
マスの名称