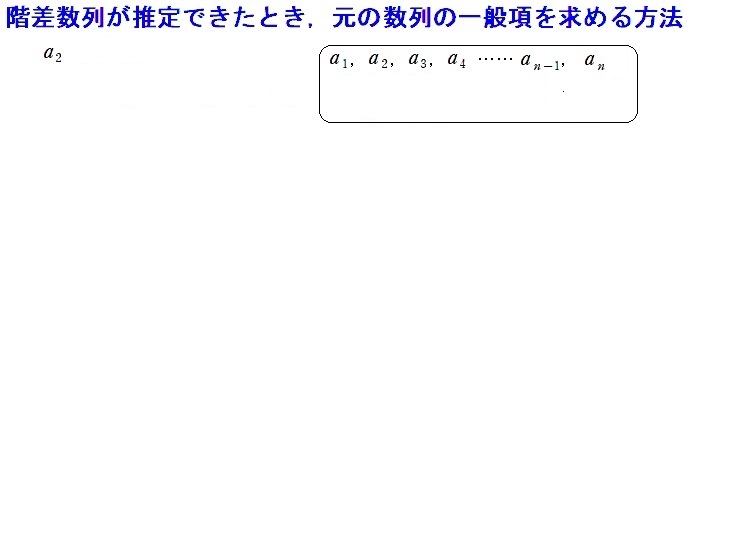
階差数列について

上の変形が出来なくても，今は気にしなくてよい。

練習です。次の数列の階差数列の，初項から第 5 項までを穴埋めしてください。(半角で入力)

元の数列 3， 4， 6， 9， 13， 18 　 階差数列 元の数列 3， 4， 2， 6， -2， 14 　 階差数列

a1=	12 - 1 + 6	= 3		← n の値を変えて遊ぶことが出来ます。 最初の数列のとおりに並ぶことを確認してください。
	2

a1=	10 - (-2)1-1	=	10 - (-2)0	=	10 -1	= 3		← n の値を変えて遊ぶことが出来ます。 最初の数列のとおりに並ぶことを確認してください。
	3		3		3

元の数列が列挙されている場合，階差数列は，等差数列か等比数列のどちらになるのか，必ず確認してください。 公比が正の等比数列は，気づきにくいようです。色々自分で練習してみて、気づきにくいものから確認すれば良いと思います。 推定ができなかったら再び階差をとるのですが、これは大変難しいことので，割愛します。 同内容の Youtube 動画は、こちら