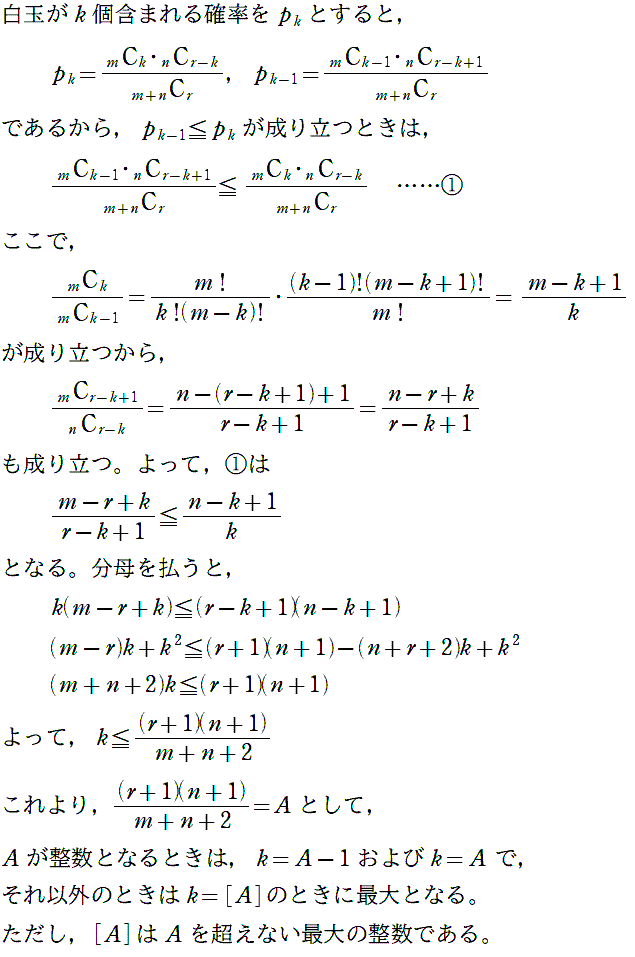確率の最大値について

試行とその事象によっては，増加し続けることも，減少し続けることもありまし，そもそも同様に確からしいこともあります。
ここで扱うのは，一定の値までは増加し続け，それ以降は減少し続けるもののみとします。
世間一般では「確率の最大値」と題されていますが，本当に最大値を求めるのではなく，
確率が最大となるときの事象の値を求めることがほとんどです。

ある試行に対し，事象 k の起こる確率を p_k とする。
p₁ ＜ p₂ ＜・・・＜ p_{k - 1} ＜ p_k かつ，p_k ＞ p_k＋1 ＞・・・
が成り立つとき，p_k が求める最大値である。

例題 1 　1 個のさいころを n 回投げて，3 の倍数の目の出る回数の確率が最大となるのは何回のときか調べる。
(1)　n＝10 のときを調べよ。 (2)　n＝20 のときを調べよ。

例題 1	1 個のさいころを n 回投げて，3 の倍数の目の出る回数の確率が最大となるのは何回のときか調べる。 (1)　n＝10 のときを調べよ。 (2)　n＝20 のときを調べよ。

例題 2 　白玉 13 個，赤玉 17 個の入った袋から 7 個を同時に取り出すとき，白玉が k 個取り出される確率を p_k とする。
p_k の値が最大になるときの k の値を求めよ。

例題 2	白玉 13 個，赤玉 17 個の入った袋から 7 個を同時に取り出すとき，白玉が k 個取り出される確率を p_k とする。 p_k の値が最大になるときの k の値を求めよ。

一般 1 　1 度の試行で事象 A の起こる確率が p であるとし，この試行を n 回繰り返すとき，
A がちょうど k 回起こる確率を p_k とする。
p_k が最大となるときの k の値を n，p で表せ。

一般 1	1 度の試行で事象 A の起こる確率が p であるとし，この試行を n 回繰り返すとき， A がちょうど k 回起こる確率を p_k とする。 p_k が最大となるときの k の値を n，p で表せ。

n 回繰り返す反復試行において，事象 A がちょうど k 回起こる確率が最も高いとすると，
k の値は A の起こる回数の期待値 pn と非常に近い値であることが知られています。
例題 1 (1)の回数の期待値は 10/3 ≒ 3.33，(2) の回数の期待値は 20/3 ≒ 6.67 ですから，
回数を多くするとさらに近づくことが予想できます。
参考：A の起こる回数の期待値の証明

一般 2 　白玉 n 個，赤玉 m 個の入った袋から r 個を同時に取り出すとき，
白玉が取り出される確率が最大となるのは何個のときか。

一般 2	白玉 n 個，赤玉 m 個の入った袋から r 個を同時に取り出すとき，白玉が取り出される確率が最大となるのは何個のときか。

目次へ