完全順列は,正式には攪乱(かくらん)順列と呼ばれます。(出典:新数学辞典)
例えば,次のように並んだものは完全順列の 1 つです。
| (番号) | (1) | (2) | (3) | (4) | (5)
|
|---|
| 札 | 3 | 4 | 1 | 5 | 2
|
|---|
ある程度までは樹形図を作ったほうが早そうですが,ここでは一般の n 枚の拡張を試みます。
n 枚の札で完全順列が an 通り作れるとすると,
1 枚では無理なので a1 = 0,a2 = 1 です。
また,ここでは,札の数字と順番が同じとき,「同じ番号にある」と表現することにします。
当たり前かもしれませんが,n 枚のうち 2 枚以上の札が同じ番号にあるとき,
n + 1 枚目の札をどの札と取り換えても,少なくとも 1 枚の札が同じ番号にとどまります。
これより,n + 1 枚目の札を追加するときに完全順列が作れる条件は,
n 枚の札のうち,同じ番号にあるものは 1 枚以下であることになります。
[A] n 枚が完全順列をなしているとき
n + 1 枚目の札を追加するとき,どの札と入れ替えても完全順列の 1 つが出来上がります。
(下の例は 7 枚目を追加したところ)
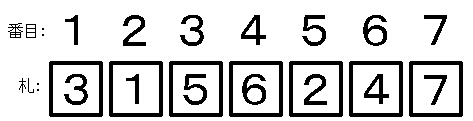
よって,このときは nan 通り作れます。
[B] n 枚のうち,ちょうど 1 枚が同じ番号にあるとき
n + 1 枚目の札を追加して完全順列を完成させるには,同じ番号にある札と交換するしかありません。
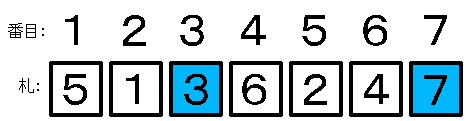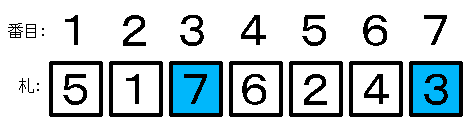
どの札が同じ番号にあるかの札の選び方は n 通りあるから,
このときは nan-1 通り
以上より、次のような漸化式が作れます。
a1 = 0,a2 = 1,an + 1 = nan + nan-1 ……① (n ≧ 2)
①の両辺から (n + 1)an を引くと,
an + 1 - (n + 1)an = -an + nan-1
すなわち,
an + 1 - (n + 1)an = -(an - nan-1) ……②
ここで,bn = an - nan-1 とおくと,②は
bn + 1 = -bn
となるから,数列 {bn} は公比 -1 の等比数列です。
また,b1 = a2 - a1 = 1 より,
bn = (-1)n
よって,
an - nan-1 = (-1)n
両辺を n! で割ると,
| an | - | nan-1
| = | (-1)n | ……③
| | n! | (n -1)! | n!
|
すなわち,
| cn + 1 - cn = | (-1)n + 1
| | (n + 1)!
|
n ≧ 2 のとき,
cn = 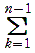
| (-1)k + 1
| | (k + 1)!
|
となります。右辺を少し観察すると,
| となり,これに | 1 | - | 1 | (= 0) を加えても値が変わらないことから,
| | 0! | 1!
|
cn = 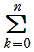
| (-1)k
| | k!
|
残念ながら右辺をこれ以上簡単にすることはできませんが,
| an | = 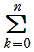
| (-1)k | ……④
| | n! | k!
|
となります。
ところで,ex のマクローリン展開は,
ex = 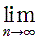 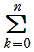 | xk
| | k!
|
となることが知られています。この式の両辺に x = -1 を代入すると,
e-1 = 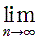 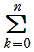 | (-1)k
| | k!
|
これは,n を限りなく大きくすると,完全順列になる確率が e-1 に収束することを示しています。
スクリプトによる攪乱順列計算機
個の攪乱順列の場合の数は
神戸大学の入試問題にチャレンジ!
|