立方体の塗りわけ方法について考えます。
全ての例題について，次の条件を満たすものとします。
＊ 指定された色より多い色は用意しない。
＊ 回転させると一致する塗り方は同じものとする。
＊ 各面は 1 色のみを用いて塗るものとする。
|
例題 1 立方体の各面をちょうど 6 色で塗り分ける方法は何通りあるか。
|
立体についても「固定して考える」のは同じです。
例えば A，B，C，D，E，F の 6 色で塗るとすると，
上面は F と固定してしまいます。
F の裏面に塗る色の決め方は 5 通り
残りの 4 色は円順列ですから，(4 - 1)! = 6 （通り）
以上より，全部で 30 通り
つかめないときは，下のスライドを見て，ゆっくり理解しましょう。
|
例題 2 立方体の各面をちょうど 2 色で塗り分ける方法は何通りあるか。
|
[a] 1 面 + 5 面と塗るとき
1 面しか塗らないほうの色の選び方は 2 通り
のこりはすべて他方の色となるから，2 通り
[b] 2 面 + 4 面と塗るとき
2 面使う方の選び方は 2 通り
2 面使う方の面のぬり方は，隣り合うか，向かい合うかの 2 通り
以上より，[b] の塗り方は 4 通り
[c] 3 面ずつ塗るとき
塗り方は，＜向かい合う面がすべて異なる色である＞
または＜向かい合う面のうち， 1 組だけ異なる色である＞の 2 組がある。
＜参考：＞上記 2 通りの展開図
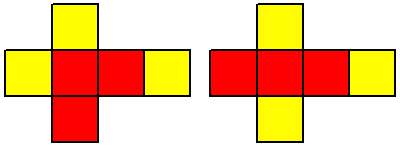[a]，[b]，[c] より，全部で 8 通り。
|
例題 3 立方体の各面をちょうど 3 色で塗り分ける方法は何通りあるか。
|
[a] 1 面 + 1 面 + 4 面と塗るとき
4 面塗られる色の選び方は 3 通り
塗り方について，1 面ずつ塗る色の面が向かい合うか，隣り合うかの 2 通り
以上より，[a] の塗り方は 6 通り
[b] 1 面 + 2 面 + 3 面と塗るとき
色の選び方は 3! = 6 （通り）
上面を 1 面しか使わない色で固定し，2 面使う色を B，3 面使う色を C とする。
[b1] 底面が B のとき，側面の塗り方は BCCC の 1 通り
[b2] 底面が C のとき，側面のぬり方は，BBCC，BCBC の 2 通り
以上より，[b] の塗り方は 6 × 3 = 18 通り
[c] すべての色を 2 面ずつ塗るとき
[c1] 向かい合う面が 3 組とも同じ色のとき，1 通り
[c2] 向かい合う面の 1 組だけが同じ色のとき
この色の選び方は 3 通りあり，側面の塗り方は BBCC の 1 通り
[c3] 3 色とも隣り合う面に塗るときは 2 通り（下の展開図を参照）
以上より，[c] の塗り方は 6 通り
[a]，[b]，[c] より，ちょうど 3 色で塗り分ける方法は，6 + 18 + 6 = 30 （通り）
|
例題 4 立方体の各面をちょうど 4 色で塗り分ける方法は何通りあるか。
|
用いる色を A，B，C，D とします。
| [a]
| 1 + 1 + 1 + 3 （面）と塗るとき
3 面塗られる色の選び方は 4 通り（これを D とする）
また，残った色を A，B，C とし，上面を A で固定する。
[a1] 底面が B のとき，側面は CDDD の 1 通り
[a2] 底面が C のとき，側面は BDDD の 1 通り
[a3] 底面が D のとき
側面の B を固定すると，残りはCDD の並べ方の 3 通りある。
以上より，[a] の塗り方は 4 × (1 + 1 + 3) = 20 （通り）
| | [b] |
1 + 1 + 2 + 2 （面）と塗るとき
1 面しか塗られない色の選び方は，4C2 = 6 （通り）
仮に ABCCDD と塗るとして，A を上面に固定する。
[b1] 底面が B のとき，側面の塗り方は CCDD，CDCD の 2 通り
[b2] 底面が C のとき，側面の B を固定すると，残りは CDD の並べ方となるから，3 通り
[b3] 底面が D のとき，[b2] と同様に 3 通り
以上より，[b] の塗り方は，6 × (2 + 3 + 3) = 48 （通り）
|
[a]，[b] より，ちょうど 4 色で塗り分ける方法は，20 + 48 = 68 （通り）
|
例題 5 立方体の各面をちょうど 5 色で塗り分ける方法は何通りあるか。
|
2 面に塗られる色の選び方は 5 通り
1 面しか塗らない色の 1 つを上面に固定し，残った色を ABCDD とする。
[a] D が底面のとき
側面の並べ方は，(4 - 1)! = 6 （通り）
[b] D 以外が底面のとき
底面の色の選び方は 3 通り
側面の塗り方は 2 面が同じ色であるから，3 通り
以上より，[b] の塗り方は 9 通り
[a]，[b] より，ちょうど 5 色で塗り分ける方法は，5 × (6 + 9) = 75 （通り）
場合の数を小さい順に並べると，
1 色 ＜ 2 色 ＜ 3 色 = 6 色 ＜ 4 色 ＜ 5 色
となりました。この並びは少し意外でした…
| 