カタラン数

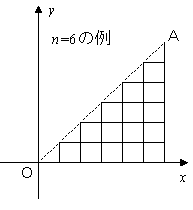
例題
動点Ｐは座標平面上をx軸の正の方向またはy軸の正の方向へ１進むことを繰り返す。
nを正の整数とし、点Ｐが原点Ｏ(0,0)を出発して点Ａ(n,n)に進む最短経路のうち、
y座標の値がx座標の値より大きくなることが１度もないものは何通りあるか。
n=4のときで実験してみます。
題意を満たすように動かそうとすると初手は必ず点(1,0)へ動くのですが、
それでは「辺」の数が１つ減り考えにくくなるので、
まずは(0,1)へ動くものも許して全体を数えると、
8Ｃ4＝70通りあります。
直線y=x+1を l とし、題意を満たさないものを漏れなく
重複なく取り出すことを考えます。
すると、右の図でX0、…X3を
初めて通るものを抜き出していけばよいことに気づきました。
それらを、初めて点Xkに達した先から l に関して
対称に移動させてみたものを並べてみると、以下のとおりになります。
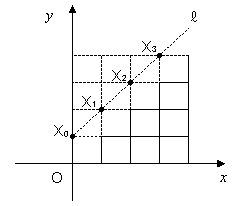
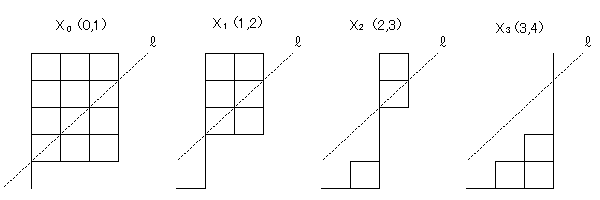
４つの図形を重ねてみると、見事に５×３の長方形が出来上がります。
本当にそうなのか、ぱたぱたアニメで確認してみましょう。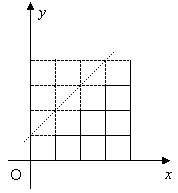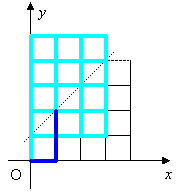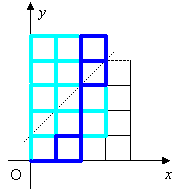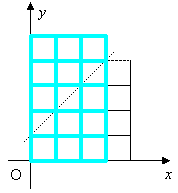
以降n≧5のときも、題意を満たさないものを同じルールで折り返すと、
(n+1)×(n-1)の長方形の対角を結ぶ最短経路の道順の個数と一致します。
よって、一般には次の公式が成り立ちます。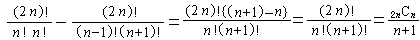

参考サイト＜水の流れ−カタラン数と最短経路について−＞

目次へ